
 |
 |
 |
 |
|
|||
Static typing and other mysteries of lifeBertrand Meyer, ISE Inc.NOTE: This is the text of Meyer's keynote lectures given in 1995 at the OOPSLA and TOOLS PACIFIC conferences. For an up-to-date and complete discussion see chapter 17 (Typing) of the book Object-Oriented Software Construction, second edition (Prentice Hall, 1997). *************** Serious use of object technology requires static typing. This paper explains why, shows the set of facilities that are needed to make static typing possible, and presents a solution to the principal issue of static typing (covariance and descendant hiding). *************** The concept of static typing is very simple -- a consequence of the simplicity of the object-oriented model of computation. If one puts aside the details of an object-oriented language, necessary to write realistic software but auxiliary to the basic model, only one kind of event ever occurs during the execution of an object-oriented system: routine call. In its general form it may be written, using the syntax of Simula and Eiffel, as x.f (arg) meaning: execute on the object attached to x the operation f, using the argument arg, with the understanding that in some cases arg stands for several arguments, or no argument at all. Our Smalltalk friends would say "pass to the object x the message f with argument arg", and use another syntax, but those are differences of style, not substance. At run time, this is what our systems do: calling features on objects, passing arguments as necessary. That everything relies on this canonical scheme accounts in part for the general feeling of beauty that object-oriented ideas arouse in many people. From the simplicity of the model follows the simplicity of the typing problem, whose statement mirrors the structure of the Basic Construct:
______________________________________________________________
When, and how, do we know that:
1 There is a feature corresponding to f and applicable to the object?
2 arg is an acceptable argument for that feature?
______________________________________________________________
The policy known as static typing, which I will argue is the only reasonable one for professional software development, states that we should answer the "when" part of the question by "before we ever think of running the system", and the "how" part by "through mere examination of the software text". 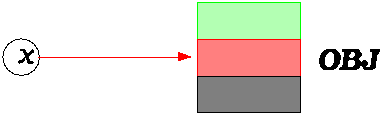
Let us make the terminology precise. x will be called an entity; this is a generalization of the traditional notion of variable. f will, in interesting cases, be a routine; Smalltalk would call it a method, but there is no need for a new term since the older one is well established. At run time the value of x, if not void, will be attached to a certain object, OBJ on the preceding figure. Readers already familiar with the issues of typing will perhaps appreciate a preview of the conclusion. It can be expressed in reference to a conjecture that Pierre America from Philips Research Laboratories expressed in a panel on the topic at TOOLS EUROPE a few years ago. America stated that three properties are desirable: static typing, substitutivity, and covariance; his conjecture is that one can achieve at most two of them. The aim of the present work is to disprove the America conjecture and show that we can enjoy static typing and covariance while preserving substitutivity when it is needed and safe. If you do not completely understand these terms do not worry; they will be explained shortly. Starting now with the basic concepts we must first make sure to avoid any misunderstanding. Beginners with a Smalltalk background sometimes confuse static typing with static binding. Two separate questions are involved. Typing, as noted, determines when to check that the requested routine will be applicable to the requested object; binding determines what version of the feature to apply if there is more than one candidate. For example in a hypothetical inheritance hierarchy shown on the figure below, we might have the feature lower_landing_gear defined only at the level of PLANE, not at the general level of AIRCRAFT: 
Then for a call of the form my_aircraft.lower_landing_gear two separate questions arise: when to ascertain that there will be a feature lower_landing_gear applicable to the object; and, if there is more than one, which one to choose. The first question is the typing question, the second is the binding question. Both answers can be dynamic, meaning at execution time, or static, meaning before execution. Static binding, which if I understand properly is the default C++ policy, would mean that we disregard the object type and believe the entity declaration, leading us for example to apply to a Boeing 747-400 the version of a feature, such as lower_landing_gear, that has been defined for the standard Boeing 747 planes. This does not seem right, so we should choose dynamic binding, defined simply as applying the right feature. Dynamic binding, as many of you undoubtedly know, is crucial in ensuring the decentralized, evolutionary system architectures made possible by the object-oriented method. Dynamic binding does not imply dynamic typing. Typing is about something else: when to determine that there will be at least one feature applicable to the object. Dynamic typing, as in Smalltalk, means waiting until the execution of the feature call to make that determination. Static typing, as in Eiffel, means performing the check before any execution of the software; typically, this will be part of the verifications made by a compiler. It is hardly necessary to emphasize the importance of static typing. Anyone concerned with software reliability knows how much more expensive it is to detect errors late in the lifecycle. This is confirmed quantitatively by Barry Boehm's well-known studies: 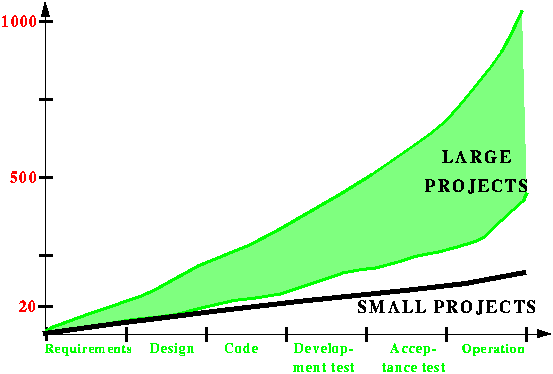
This insistence that the language should permit static type checking is one of the major differences between Eiffel and Smalltalk, and the Smalltalk policy is one of the reasons why I think Smalltalk is inappropriate for serious industrial developments. After all, run time is a little late to find out whether you have a landing gear. For static type checking to be possible, the language must be designed accordingly. Here are the basic rules as they exist in Eiffel, which at first sight seem to allow a compiler, global or incremental, to ascertain type safety. More details can be found in the official reference on Eiffel: the book Eiffel: The Language (Prentice Hall, 1992). Simplifying a little, there are three rules; one applies to declarations, the second to feature calls, and the third to attachments, that is to say assignments and argument passing. First, we require that every entity be declared with a certain type: ______________________________________________________________ Declaration rule Every entity must be declared as being of a certain type. ______________________________________________________________ For example: x: AIRCRAFT; Only to the inexperienced will this appear to be constraining. Seasoned software engineers know that software written once is read and rewritten many times, and that the small effort of declaring the type of every entity is generously repaid by the readability that such declarations bring to the software text. Next, for what we have called the basic operation of object-oriented computing, we require that any feature call use a feature that exists in the base class of the target x:
______________________________________________________________
Call rule
If a class C contains the call
x.f (...)
there must be a feature of name f in the base class of the type
of x, and that feature must be available (exported) to C.
______________________________________________________________
This is easy to determine thanks to the preceding rule, which causes the type of x to be known clearly and unambiguously to anyone who reads the class text. (A note for readers familiar with C++: in that language the term "base class" is used in the sense of parent class. Here "base class" is the Eiffel term denoting the class on which a type is based. For example a non-generic class C is its own base class; for a type D [T], where D is a generic class, the base class is D.) Finally, we have a rule regarding attachment: for any assignment of an expression y to an entity x, the type of y must be compatible with the type of x.
______________________________________________________________
Attachment rule
In an assignment x := y, or the corresponding argument passing,
the base class of the type of y must be a descendant of that of x.
______________________________________________________________
In a classical language such as Pascal or Ada, this would mean that the types are identical. Thanks to inheritance the requirement is more flexible here: the type of y may be any descendant, in the sense of inheritance, of the type of x. The same rule applies to the case in which x is a formal argument to a routine and y is the corresponding actual argument in a call. The term "attachment" covers both cases -- assignment and actual-to-formal association. In a simple world these rules would suffice. They are easy for a software developer to understand, and easy for a compiler to implement. In particular, the compiler can check them incrementally. One of the achievements of ISE's Eiffel compiler development, known as the Melting Ice technology (as part of the EiffelBench graphical development environment) has been to show that it is possible to guarantee type checking and efficient code generation, as in compiled environments, while avoiding the long edit-compile-link-execute cycles traditionally required in such environments; using Eiffel, one can get the fast turnaround that people have come to associate with Lisp and Smalltalk while preserving efficient code generation and static type checking. Strangely enough, one encounters objections to the static typing approach. These objections do not hold on further examination, but they do highlight the set of properties that must be satisfied by a realistic use of static typing. First, there is no such thing as "a little bit statically typed", any more than "a little bit pregnant". Either the language is statically typed or it is not. The C++ approach, where you can still "cast" -- that is to say convert -- a value into just about any type, defeats in my view the principle of static typing. For one thing, it makes garbage collection, a required component of serious object-oriented computing, very difficult if not impossible. Second, a statically typed language requires multiple inheritance. The objection against typing often heard from people with a Smalltalk background is that it prevents one from looking at objects in different ways. For example an object of type DOCUMENT might need to be transmitted over a network, and so will need the features associated with objects of type MESSAGE. 
But this is a problem only in languages such as Smalltalk that do not permit multiple inheritance. Multiple inheritance, of course, must be handled properly, with mechanisms as in Eiffel for taking care of name clashes, conflicting redefinitions, and potential ambiguities in repeated inheritance. I mention this because one still encounters people who have been told that multiple inheritance is tricky or dangerous; such views are usually promoted by programmers using languages that do not permit multiple inheritance, and are about as convincing as opinions on sex emanating from the Papal nuncio. Next, static typing requires genericity, so that we can define flexible yet type-wise safe container data structures. For example a list class will be defined as class LIST[G] ... Genericity in some cases, needs to be constrained, allowing us to apply certain operations to entities of a generic type. For example if a generic class VECTOR has an addition operation, it requires an addition also to be available on entities of type G, the generic parameter. This is achieved by associating with G a generic constraint NUMERIC: class VECTOR [G --> NUMERIC] ... meaning that any actual generic parameter used for VECTOR must be a descendant of this class NUMERIC, which has the required operations such as "plus" and "minus". We also need a mechanism of assignment attempt. This makes it possible to check that a certain object, usually obtained from the outside world, for example a database or a network, has the expected type. The assignment attempt x ?=y will assign to x the value of y if it is of a compatible type, but otherwise will make x void. This instruction is one of the Eiffel inventions of which we can be proudest. Some of you may be familiar with a similar mechanism that has more recently been proposed for C++ under the name type-safe downcasting. Also necessary are assertions, associated, as part of the idea of Design by Contract, with classes and features. Assertions make it possible to describe the semantic constraints which cannot be captured by type specifications. Finally, a realistic object-oriented type system will require two mechanisms that will be described in more detail shortly: covariance, which governs how we can redefine the signatures of routines, and anchored declarations, of the form y: like x which avoid endless type redeclarations. Ideally, a presentation of typing should stop here. Unfortunately, the combination of static typing with other requirements of the object-oriented method makes the issues more difficult than they appear at first. To accompany the discussion it will be convenient to use the example hierarchy shown below, applying to a high-school ski team preparing for a trip to a minor-league championship. For brevity and simplicity we use the class names GIRL as an abbreviation for "member of the girls' ski team" and BOY as an abbreviation for "member of the boys' ski team". Some skiers in each team are ranked, that is to say have already recorded good results in earlier championships. This is an important notion: ranked skiers will start first in a slalom, giving them a considerable advantage over the others; after too many competitors have used it, the run is much harder to negotiate. (This rule that ranked skiers go first is a way to privilege the already privileged, and may explain why skiing holds such a fascination over the minds of many people: that it serves as an apt metaphor for life itself.) This yields two new classes, RANKED_GIRL and RANKED_BOY. I hope this example will provide a welcome relief from the omnivores and herbivores that have for too long grazed the wild pastures of such Usenet forums a scomp.object. 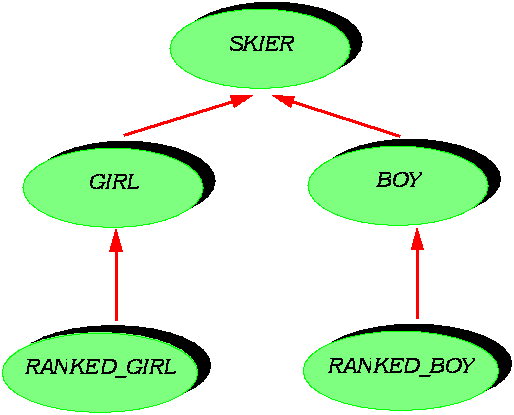
To assign the rooms we may use a parallel hierarchy; some rooms will be reserved for boys only, girls only, or ranked girls only. Here is an outline of class SKIER: class SKIER feature roommate: SKIER; -- This skier's roommate share (other: SKIER) is -- Choose other as roommate. require other /= Void do roommate := other end ... end-- class SKIER We have two features of interest: the attribute roommate; and the procedure share, which makes it possible to assign a certain skier as roommate to the current skier. Note the use of Eiffel's assertions: the require clause introduces a precondition stating that the argument must be attached to an object. A typical call, as in s1, s2: SKIER; ... s1.share (s2) will enable us to assign a certain roommate to a certain skier. How does inheritance get into the picture? Assume we want girls to share rooms only with girls, and ranked girls only with ranked girls. We will redefine the type of feature roommate, as shown by the figure: 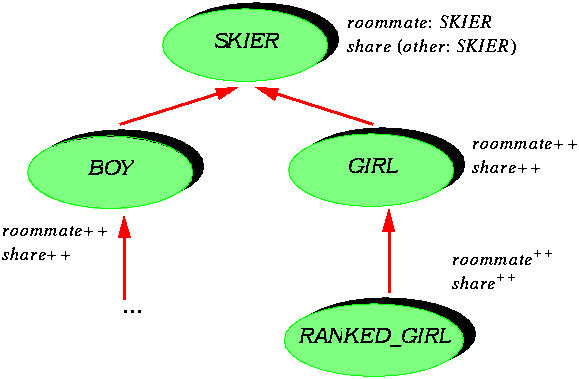
class GIRL inherit SKIER redefine roommate end feature roommate: GIRL; -- This skier's roommate ... end -- class GIRL We should correspondingly redefine the argument to procedure share, so that a more complete version of the class text is: class GIRL inherit SKIER redefine roommate, share end feature roommate: GIRL; -- This skier's roommate share (other: GIRL) is -- Choose other as roommate. require other /= Void do The preceding figure, repeated below for convenience, illustrates these classes. 
++, a B.O.N. notation, means "redefined". Since inheritance is specialization, the type rules naturally require that if we redefine the result of a feature, here roommate, the new type must always be a descendant of the original one. We should correspondingly redefine the type of the argument other of routine share. This is the policy known as covariance, where the "co" indicates that the argument and result vary together. The reverse policy is termed contravariance. I believe that this terminology was introduced by Luca Cardelli. Strangely enough, some workers in the field have been advocating a contravariant policy. Here it would mean that if we go for example to class RANKED_GIRL, where the result of roommate is naturally redefined to be of type RANKED_GIRL, we may for the argument of routine share use type GIRL, or, rather scaringly, SKIER of the most general kind. One type that is never permitted in this case is RANKED_GIRL! Here is what, under various mathematical excuses, some professors have been promoting. No wonder teenage pregnancies are on the rise. As far as I understand, by the way, the C++ policy is to bar any type redefinition whatsoever -- novariance as it is sometimes called. This does not seem very useful. Covariance, of course, is not without its problems. Before looking at them we should examine a fundamental simplification. It is extremely tedious to have to redefine share the way we did in class GIRL. This redefinition only changes the type of the argument other; the rest of the routine, assertions and body, is just replicated. Anchored declarations, another Eiffel invention, addresses this problem. In class SKIER we can prepare for such redefinitions by declaring other as being of type like roommate. This is the only difference with the previous version: class SKIER feature roommate: SKIER; -- This skier's roommate share (other: like roommate) is -- Choose other as roommate. require other /= Void do roommate := other end ... end -- class SKIER Such a like declaration, known as an anchored declaration, means that other is treated in the class itself as having the same type as the anchor, here SKIER; but in any descendant that redefines roommate then other will be considered to have been redefined too. One can say without fear of exaggeration that without anchored redeclarations it would be impossible to write realistic typed object-oriented software. But what about the problems of covariance? They are caused by the clash between this concept and polymorphism. Polymorphism is what makes it possible to attach to an entity an object of a different type. It is made possible by the attachment rule introduced earlier: in the assignment x := y, the type of y may be a descendant of that of x. But with covariance this may get us into trouble. Assume we have entities s1 of type SKIER, b1 of type BOY and g1 of type GIRL; the names should be mnemonic enough: s1: SKIER; b1: BOY; g1: GIRL; In creation instructions, marked with double exclamation marks, we create two objects of types BOYand GIRL and attach them to b1 and g1 respectively: -- Create a "boy" and a "girl" objects: create b1 ; create g1; Then polymorphism allows us to let s1 represent the same object as b1: s1 := b1 Then the feature call s1.share (g1) achieves what all of us boys always dreamed of in high school, and what all parents fear. A similar problem arises out of a very important inheritance mechanism: descendant hiding, the ability for a class not to export a feature that was exported by one of its parent. 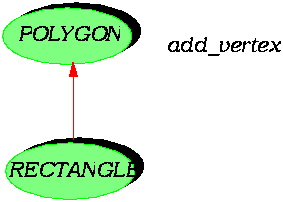
A typical example is a feature add_vertex, which class POLYGON exports but its descendant RECTANGLE hides, because it would violate the invariant of the class:
class RECTANGLE inherit
POLYGON
export {NONE} add_vertex end
feature
...
invariant
vertex_count = 4
end
The invariant is expressed here in Eiffel syntax as vertex_count = 4. Another well-known example, more academic in nature, is a class OSTRICH that inherits from a class BIRD that was equipped with a routine fly. Clearly OSTRICH should not export that routine. I should note in passing that some people criticize such practices as incompatible with a good use of inheritance. They are deeply wrong. It is a sign of the limitations of the human ability to comprehend the world -- similar perhaps to undecidability results in mathematics and uncertainty results in modern physics -- that we cannot come up with operationally useful classifications without keeping room for some exceptions. Descendant hiding is the crucial tool providing such flexibility. Hiding add_vertex from RECTANGLE or fly from OSTRICH is not a sign of sloppy design; it is the recognition that other inheritance hierarchies that would not require descendant hiding would inevitably be more complex and less useful. Like covariance, then, descendant hiding is made necessary by the modeling requirements of the object-oriented method. But like with covariance this modeling power causes a conflict with the tricks made possible by polymorphism. An example is trivial to build; here is one: p: POLYGON; r: RECTANGLE; create r; ... p := r; ... p.add_vertex The triviality of these examples makes up what we may call the static typing paradox. A student can make up a counter-example showing a problem with covariance or descendant hiding in a few minutes; yet Eiffel users universally report that they almost never run into such problems in real software development. This is certainly confirmed by our own practice, even though the ISE Eiffel environment represents about half a miillion lines of Eiffel and about 4000 classes. But of course this does not relieve us from the need to find a theoretical and practical solution. The problem has been discussed several times in the literature. William Cook discussed it in a paper at the 1989 ECOOP conference. At TOOLS 1992 in Dortmund Franz Weber proposed a solution based on adding a generic parameter for each problematic type. In chapter 22 of the book Eiffel: The Language a solution was described which is based on determining the set of all possible dynamic types for an entity. So we would for example find out that s1 can have BOY among its dynamic types and hence disallow the call s1.share (g1). This approach is theoretically correct but has not been implemented since it requires access to the entire system; so rather than a mechanism to be added to an incremental compiler it is a kind of lint that should be applied to a finished system. Incremental algorithms seem possible, but they have not been fully demonstrated. The new approach that I think is the right one is paradoxical in that it is more pessimistic than the earlier one. In general, typing is pessimistic. To avoid some possibly failed computations, you disallow some possibly successful computations. In Pascal, for example, assigning 0.0 to an integer variable n would always work; assigning 1.0 would probably work; assigning 3.67 would probably not work; but assigning 3.67 -- 3.67 would actually work. Pascal cuts to the essentials by disallowing, once and for all, any assignment of a floating-point value to an integer variable. This is a pessimistic but safe solution. The question is how pessimistic we can afford to be. For example we can have a guaranteeably safe language by disallowing everything, but this is not very useful. What we need is a pragmatic assessment of whether the type rules disallow anything that is really needed by real programs. In other words a set of typing rules should be sound and useful. "Sound" means that every permitted text is safe. "Useful" means that every desirable computation can still be expressed without a violation of the type rules. I believe that the rules which follow satisfy these two properties of soundness and usefulness. Here is the gist of the rules, whose full formal details may be found by following the link to "the complete typing rules" on our Web site. A full discussion will appear in the second edition of my book Object-Oriented Software Construction. The basic two notions are "polymorphic entity" and "catcall". ______________________________________________________________ Definition: Polymorphic entity An entity x is polymorphic if it satisfies one of the following properties: + It appears in an assignment x := y, where y is of a different type or (recursively) polymorphic. + It is a formal routine argument. + It is an external function. ______________________________________________________________ An entity is polymorphic if it can be attached to objects of more than one type. The basic case is that it appears as target of an assignment whose source is of a different type or, recursively, polymorphic. We also consider --- this is the second case in the definition, and very important although very pessimistic -- that any routine argument is polymorphic, because we have no control over the actual arguments in possible calls; this rule is closely tied to the reusability goal of object-oriented software construction, where an Eiffel class is intended, eventually, to be included in a library where any client software will be able to call it. A call is polymorphic if its target is polymorphic. Next comes the definition of CAT routines and catcalls: ______________________________________________________________ Definition: Catcall A routine is a CAT (Changing Availability or Type) if some redefinition changes its export status or the type of one of its arguments. A call is a catcall if some redefinition of the routine would make it invalid because of a change of export status or argument type. ______________________________________________________________ If we look back at our examples we see that they involve catcalls on polymorphic entities, also known as polymorphic catcalls, marked by two asterisks below: create b1 ; create g1; ... s1 := b1 ... s1.share (g1) -- ** _____________________________ create r ... p := r ... p.add_vertex** Polymorphic calls are of course permissible; they represent some of the most powerful mechanisms of the object-oriented method. Catcalls are also desirable; they are, as we saw, necessary to obtain the flexibility and modeling power that we expect from the approach. But we cannot have both. If a call is polymorphic, it must not be a catcall; if it is a catcall, it must not be polymorphic. Polymorphic catcalls will be flagged as invalid. ______________________________________________________________ The new type rule Polymorphic catcalls are invalid. ______________________________________________________________ If you remember the America conjecture, we of course do not sacrifice static typing; we do not sacrifice covariance; and we do not sacrifice substitutivity, that is to say polymorphic assignments of a more specialized value to a more general entity, except in cases in which they would clash with the other rules. As evidenced by the practical Eiffel experience that was mentioned earlier, such clashes are very rare; they are signs of bad programming practices and should be banned. So this is the type rule: a prohibition of polymorphic catcalls. This rule is similar to the one in Eiffel: The Language but much, much simpler because it is more pessimistic. It is checkable incrementally: a violation will be detected either when an invalid call is added or when an invalid redefinition is made. It is also checkable in the presence of precompiled libraries whose source is not available to users. As a complement it is useful to show the robustness of this solution by giving a technique which will answer a common problem. Assume that we have two lists of skiers, where the second list includes the roommate choice of each skier at the corresponding position in the first list. We want to perform the corresponding share operations, but only if they are permitted by the type rules, that is to say girls with girls, ranked girls with ranked girls and so on. This problem or similar ones will undoubtedly arise often. An elegant solution, based on the preceding discussion and assignemnt attempt, is possible. This solution can be implemented in Eiffel right now; it does not require any language change. We will propose to the Nonprofit International Consortium for Eiffel, the body responsible for Eiffel standardization, to add to class GENERAL a new function fitted. GENERAL is a part of the Eiffel Library Kernel Standard, the officially approved interoperability basis; every Eiffel class is a descendant of GENERAL. Here is the function fitted (the name might change). fitted (other: GENERAL): like other is -- Current if other is attached to an object of -- exactly the same type; void otherwise. do if other /= Void and then same_type (other) then Result ?= Current end end Function fitted returns the current object, but known through an entity of a type anchored to the argument; if this is not possible it returns void. Note the role of assignment attempt. This function gives us a simple solution to our problem of matching skiers without violating type rules. Here is the necessary routine match: match (s1, s2: SKIER) is -- Assign s1 to same room as s2 if permissible. local gender_ascertained_s2: like s1 do gender_ascertained_s2 := s2.fitted (s1); if gender_ascertained_s2 /= Void then s1.share (gender_ascertained_s2) else "Report matching is impossible for s1 and s2" For a skier s2 we define a version gender_ascertained_s2 which has a type anchored to s1. I find this technique very elegant and I hope you will too. And of course parents concerned with what happens during the school trip should breathe a sigh of relief.
|